SELAMAT DATANG DI BLOG MATEMATIKA SMP SRI WARDHANIH: PERSAMAAN DAN FUNGSI KUADRAT

BAB II
Persamaan Kuadrat

Kompetensi Inti

3. Pengetahuan

Memahami dan menerapkan pengetahuan (faktual, konseptual, dan prosedural) berdasarkan rasa ingin tahunya tentang ilmu pengetahuan, teknologi, seni, budaya terkait fenomena dan kejadian tampak mata

4. Keterampilan

Mengolah, menyaji, dan menalar dalam ranah konkret (menggunakan, mengurai, merangkai, memodifikasi, dan membuat) dan ranah abstrak (menulis, membaca, menghitung, menggambar, dan mengarang) sesuai dengan yang dipelajari di sekolah dan sumber lain yang sama dalam sudut pandang/teori

Kompetensi Dasar

3.2 Menjelaskan persamaan kuadrat dan karakteristiknya berdasarkan akar-akarnya serta cara penyelesaiannya

3.3 Menjelaskan fungsi kuadrat dengan menggunakan tabel, persamaan, dan grafik

3.4 Menjelaskan hubungan antara koefisien dan diskriminan fungsi kuadrat dengan grafiknya

4.2 Menyelesaikan masalah yang berkaitan dengan persamaan kuadrat

4.3 Menyajikan fungsi kuadrat menggunakan tabel, persamaan, dan grafik

4.4 Menyajikan dan menyelesaikan masalah kontekstual dengan menggunakan sifat-sifat fungsi kuadrat

Assalamau`alaikum Wr Wb. salam jumpa lagi siswa hebat yang sholeh/sholeha, hari ini kalian akan mempelajari materi Persamaan dan Fungsi Kuadrat, tentunya materi ini tidak asing lagi bagi kalian karena sewaktu kalian di kelas 7 dan 8 pernah belajar tentang persamaan dan pertidaksamaan serta bentuk - bentuk persamaan. Kali ini kalian akan lebih dalam mempelajari persamaan yang salah satu variabelnya berpangkat dua ... mari kita lihat Peta Konsep dari materi yang akan kita pelajari, silahkan perhatikan dan cermati materi dibawah ini !

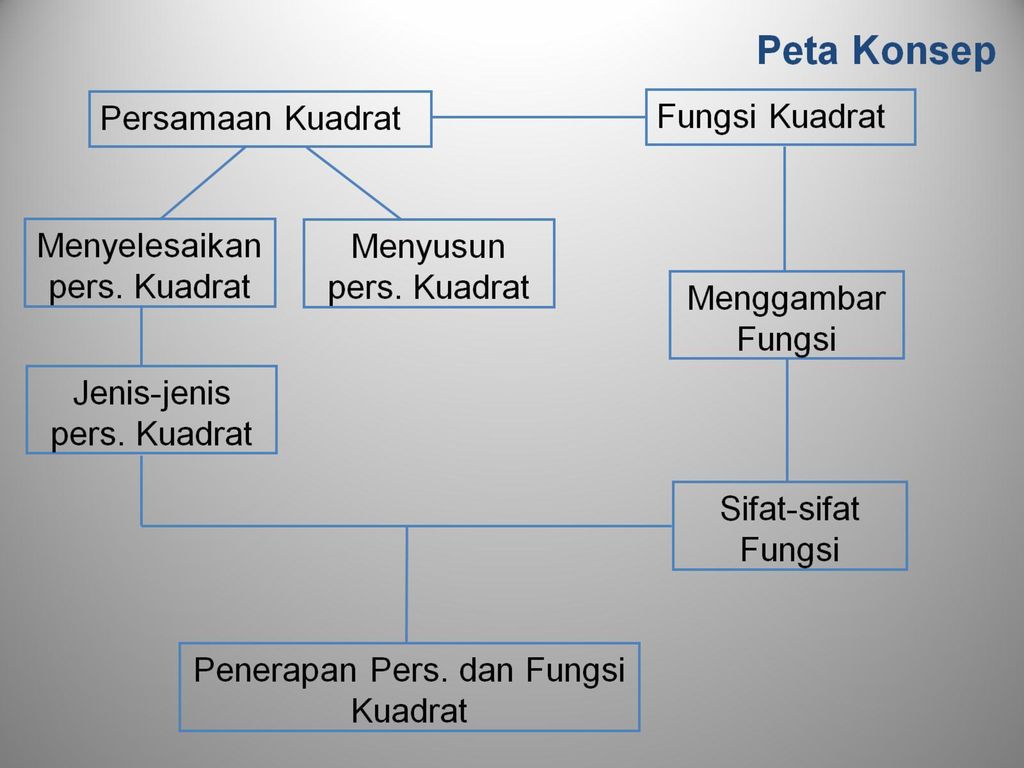
Peta Konsep. Peta Konsep F. Penerapan Persamaan dan Fungsi Kuadrat ...

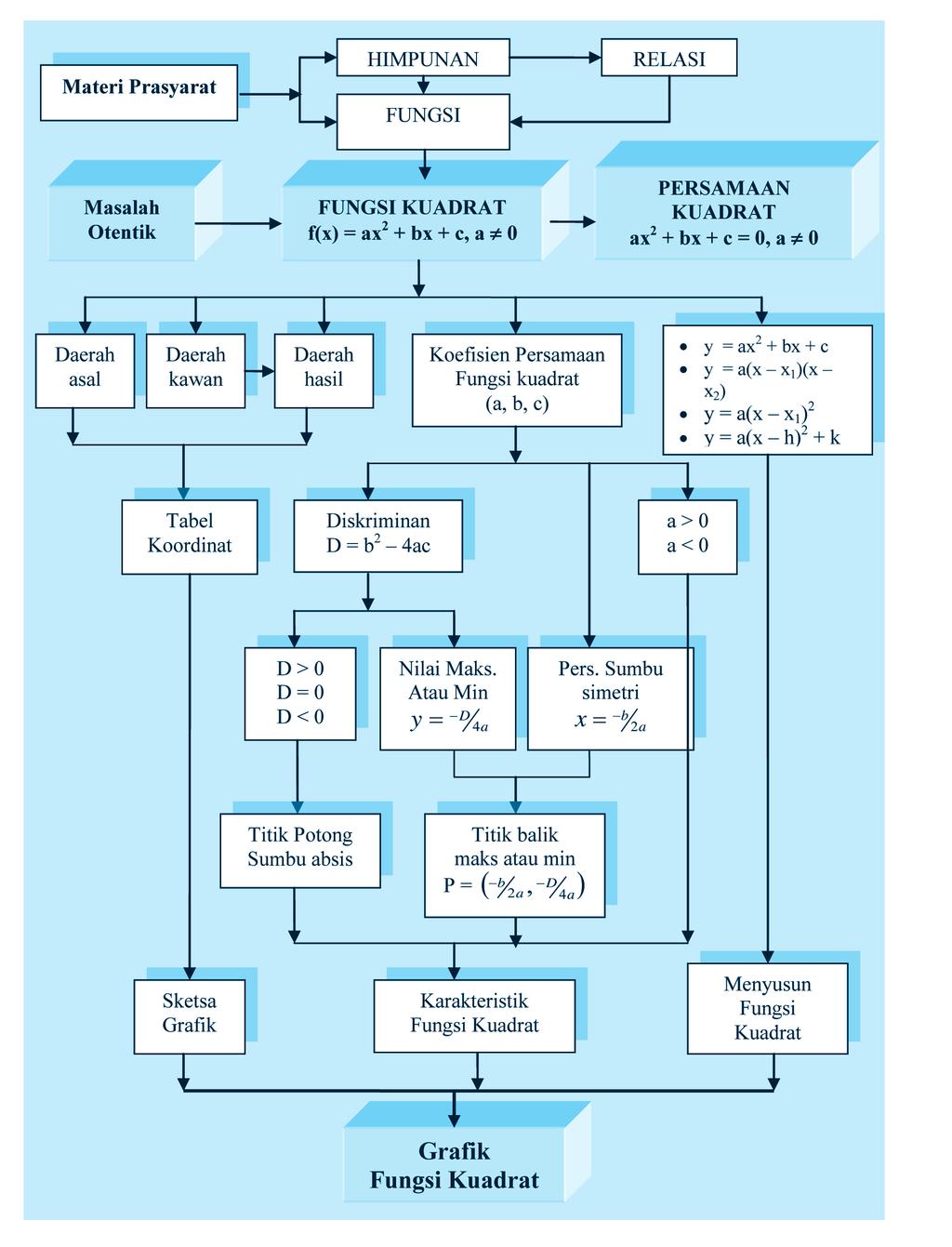
Persamaan dan Fungsi Kuadrat - PDF Free Download

Persamaan Kuadrat

Persamaan kuadrat adalah suatu persamaan polinomial berorde dua.

Bentuk umum dari persamaan kuadrat adalah ax²+ bx+ c=0 $dengan$ $a\neq 0\,\!$ Huruf-huruf a, b dan c disebut sebagai koefisien: koefisien kuadrat a adalah koefisien dari $x^{2}$ , koefisien linier b adalah koefisien dari x, dan c adalah koefisien konstan atau disebut juga suku bebas

Menyelesaikan Persamaan Kuadrat

1. Menyelesaikan persamaan kuadrat dengan pemfaktoran dilakukan dengan cara mengubah bentuk umum

ax²+bx+ c=0 menjadi bentuk faktor (x –α) (x -β)=0

Langkah-langkah penyelesaian

Ubah ke bentuk faktor (x – α) (x - β)=0
Tentukan akar-akarnya dengan (x – α)=0 atau (x - β)=0 , sehingga akar-akarnya x1=α atau x2=β.

Bentuk ini difaktorkan menjadi x (x-m) =0

Contoh :

Tentukan akar-akar persamaam kuadrat x² + 6x = 0 ;

Jawaban:

x² + 6x = 0
x(x + 6) = 0
x = 0 atau x+ 6 =0
x = 0 atau x = - 6

Bentuk ax2 +bx +c = 0 untuk a =1 , x² +bx +c = 0

Bentuk faktor dari persamaan kuadrat untuk a =1 adalah (x+α) (x+β)=0

x² + αx + βx +αβ = 0

x² + (α + β)x +αβ = 0

Perhatikan skema berikut !

Jadi persamaan kuadrat x² +bx +c = 0 dapat difaktorkan menjadi (x+α) (x+β)=0 , Jika ada bilangan a dan b sehingga (x+α) = b dan ab= c

Contoh: Tentukan akar-akar persamaan kuadrat x² –5x –24 =0

Jawaban:

Bentuk Faktor dari x² –5x –24 =0 adalah: (x -8) (x+3)=0 dimana (x-8 ) = 0 atau (x+3) = 0

Jadi , akar-akarnya adalah x = 8 atau x= -3 Untuk a ‡ 1 , ax² +bx +c = 0 dapat difaktorkan jika ada bilangan a dan b sehingga (a+b) = b dan ab= ac Bentuk faktor dari persamaan kuadrat untuk a ¹1 adalah a (x+ ) (x+ ) = 0

Contoh 2 : Tentukan akar-akar persamaan kuadrat 3x² +7x +2 =0

Jawaban (3x +1) (x+2)=0

(3x+1)=0 atau (x+2)=0 Jadi , akar-akarnya adalah x = -1/3 atau x = -2

2. Penyelesaian persamaan kuadrat dengan kuadrat sempurna

Tidak semua persamaan kuadrat mudah difaktorkan, hanya persamaan kuadrat yang akarnya rasional saja yang mudah difaktorkan. Persamaan kuadrat yang sulit difaktorkan

dapat diselesaiakn dengan kuadrat sempurna atau rumus kuadrat. Persamaan kuadrat dapat diubah kebentuk kuadrat sempurna

yaitu x²= p atau (x-m)² = p, Bentuk ax² + c = 0

Langkah-langkah:

Ubah ke bentuk x²= p
Tentukan akar dengan sifat

Contoh : Tentukan akar-akar persamaan kuadrat x² - 9= 0

Jawaban:

Bentuk ax² +bx + c = 0

Langkah-langkah:

Ubah ke bentuk kuadrat sempurna (x-m)²= p dengan rumus

Tentukan akar menggunakan sifat

Contoh 1:
Tentukan akar persamaan kuadrat x² + 4x –2 =0 dengan kuadrat sempurna !
Jawaban

3. Penyelesaian persamaan kuadrat dengan Rumus Kuadrat

Rumus ini juga dikenal dengan nama rumus ABC
Dapat digunakan untuk semua bentuk Persamaan Kuadrat
Menjadi alternatif terakhir jika persamaan kuadrat tidak dapat difaktorkan atau terlalu sulit dengan rumus kuadrat sempurna.

Contoh:
Tentukan akar persamaan kuadrat 2x² –3x –9 =0 dengan rumus ABC !
Jawaban:

FUNGSI KUADRAT

Fungsi kuadrat f(x) dapat juga ditulis dalam bentuk y atau $y = ax^2 + bx + c$

Dengan x adalah variable bebas dan y adalah variable terikat. Sehingga nilai y tergantung pada nilai x, dan nilai-nilai x tergantung pada area yang ditetapkan. Nilai y diperoleh dengan memasukan nilai-nilai x kedalam fungsi.

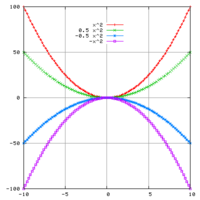
Nilai-nilai a, b dan c menentukan bagaimana bentuk parabola dari fungsi persamaan kuadrat dalam ruang xy.

a menentukan seberapa cekung/cembung parabola yang dibentuk oleh fungsi kuadrat. Nilai a > 0 akan menyebabkan parabola terbuka ke atas, sedangkan nilai a < 0 akan menyebabkan parabola terbuka ke bawah.
b menentukan kira-kira posisi x puncak parabola, atau sumbu simetri cermin dari kurva yang dibentuk. Posisi tepatnya adalah -b/2a.
c menentukan titik potong fungsi parabola yang dibentuk dengan sumbu y atau saat x = 0.

Ilustrasi grafik-grafik persamaan kuadrat dengan berbagai variasi nilai a. b dan c dapat dilihat pada gambar di atas.

Rumus kuadratis dikenal pula dengan nama rumus abc karena digunakan untuk menghitung akar-akar persamaan kuadrat yang tergantung dari nilai-nilai a, b dan c suatu persamaan kuadrat. Rumus yang dimaksud memiliki bentuk $x_{1,2}={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}$ $y=0\,\!$ . Dari rumus tersebut akan diperoleh akar-akar persamaan, sehingga persamaan semula dalam bentuk $y=ax^{2}+bx+c\,\!$ dapat dituliskan menjad $y=a(x-x_{1})(x-x_{2})\,\!$ . Dari persamaan terakhir ini dapat pula dituliskan dua hubungan yang telah umum dikenal, yaitu $x_{1}+x_{2}=-{\frac {b}{a}}\,\!$ dan $x_{1}\cdot x_{2}={\frac {c}{a}}\,\!$ .

Ilustrasi dapat dilihat pada gambar.

Dari bentuk umum persamaan kuadrat, $ax^{2}+bx+c=0\,\!$ bagi kedua ruas untuk mendapatkan $a=1$
${\frac {c}{a}}$ $x^{2}+{\frac {b}{a}}x=-{\frac {c}{a}}\,\!$ sehingga teknik melengkapkan kuadrat bisa digunakan di ruas kiri. $\left(x+{\frac {b}{2a}}\right)^{2}-{\frac {b^{2}}{4a^{2}}}=-{\frac {c}{a}}\,\!$
Pindahkan $-{\frac {b^{2}}{4ac}}$ ke ruas kanan $\left(x+{\frac {b}{2a}}\right)^{2}={\frac {b^{2}}{4a^{2}}}-{\frac {c}{a}}\,\!$
lalu samakan penyebut di ruas kanan. $\left(x+{\frac {b}{2a}}\right)^{2}={\frac {b^{2}-4ac}{4a^{2}}}\,\!$
Kedua ruas diakar (dipangkatkan setengah), sehingga tanda kuadrat di ruas kiri hilang, dan muncul tanda plus-minus di ruas kanan.

x+{\frac {b}{2a}}=\pm {\frac {\sqrt {b^{2}-4ac\ }}{2a}}

x=-{\frac {b}{2a}}\pm {\frac {\sqrt {b^{2}-4ac\ }}{2a}}

sehingga didapat rumus kuadrat

x_{1,2}={\frac {-b\pm {\sqrt {b^{2}-4ac\ }}}{2a}}

atau

x_{1,2}={\frac {-b\pm {\sqrt {D}}}{2a}}

Dalam rumus kuadrat di atas, terdapat istilah yang berada dalam tanda akar:

b^{2}-4ac,\,\!

Suatu persamaan kuadrat dengan koefisien-koefisien riil dapat memiliki hanya sebuah akar atau dua buah akar yang berbeda, di mana akar-akar yang dimaksud dapat berbentuk bilangan riil atau kompleks. Dalam hal ini diskriminan menentukan jumlah dan sifat dari akar-akar persamaan kuadrat. Terdapat tiga kasus yang mungkin:

Jika diskriminan bersifat positif, akan terdapat dua akar berbeda yang kedua-duanya merupakan bilangan riil. Untuk persamaan kuadrat dengan koefisien berupa bilangan bulat, apabila diskriminan merupakan suatu kuadrat sempurna, maka akar-akarnya merupakan bilangan rasional -- sebaliknya dapat pula merupakan bilangan irrasional kuadrat.

Jika diskriminan bernilai nol, terdapat eksak satu akar, dan akar yang dimaksud merupakan bilangan riil. Hal ini kadang disebut sebagai akar ganda, di mana nilainya adalah: $x=-{\frac {b}{2a}}.\,\!$

Jika diskriminan bernilai negatif, tidak terdapat akar riil. Sebagai gantinya, terdapat dua buah akar kompleks (tidak-real), yang satu sama lain merupakan konjugat kompleks:

x_{+}={\frac {-b}{2a}}+i\left({\frac {\sqrt {4ac-b^{2}}}{2a}}\right)

dan

x_{-}={\frac {-b}{2a}}-i\left({\frac {\sqrt {4ac-b^{2}}}{2a}}\right)

Jadi akar-akar akan berbeda, jika dan hanya jika diskriminan bernilai tidak sama dengan nol, dan akar-akar akan bersifat riil, jika dan hanya jika diskriminan bernilai tidak negatif.

Persamaan kuadrat dapat memiliki sebuah akar (akar ganda) atau dua buah akar yang berbeda, yang terakhir ini dapat bersifat riil atau kompleks bergantung dari nilai diskriminannya. Akar-akar persamaan kuadrat dapat pula dipandang sebagai titik potongnya dengan sumbu x atau garis y = 0.

Titik potong dengan garis y = d

Dengan cara pandang ini, rumus persamaan kuadrat dapat digunakan apabila diinginkan untuk mencari titik potong antara suatu persamaan kuadrat ( $y_{1}=ax^{2}+bx+c\!$ ) dengan suatu garis mendatar ( $y_{2}=d\!$ ). Hal ini dapat dilakukan dengan mengurangi persamaan kuadrat tersebut dengan persamaan garis yang titik potong antar keduanya ingin dicari dan menyamakannya dengan nol.

$\!$

Intepretasi yang sama pun berlaku, yaitu bila:

diskriminan positif, terdapat dua titik potong antara $y_{1}\!$ dan $y_{2}\!$ ,
diskriminan nol, terdapat hanya satu titik potong antara $y_{1}\!$ dan $y_{2}\!$ , dan
diskriminan negatif, tidak terdapat titik potong antara kedua kurva, $y_{1}\!$ dan $y_{2}\!$ .

Nilai-nilai y

Akar-akar suatu persamaan kuadrat menentukan rentang x di mana nilai-nilai y berharga positif atau negatif. Harga-harga ini ditentukan oleh nilai konstanta kuadrat a:

Harga-harga y
$a>0\!$ $a<0\!$
$x<x_{1}\!$ $x_{1}<x<x_{2}\!$ $x>x_{2}\!$ $x<x_{1}\!$ $x_{1}<x<x_{2}\!$ $x>x_{2}\!$
$D>0\!$ $y>0\!$ $y<0\!$ $y>0\!$ $y<0\!$ $y>0\!$ $y<0\!$
$D=0\!$ $y>0\!$ $-\!$ $y>0\!$ $y<0\!$ $-\!$ $y<0\!$
$D<0\!$ $y>0\!$ $-\!$ $y>0\!$ $y<0\!$ $-\!$ $y<0\!$

**Harga-harga y**
	$a>0\!$	$a<0\!$
$x<x_{1}\!$	$x_{1}<x<x_{2}\!$	$x>x_{2}\!$	$x<x_{1}\!$	$x_{1}<x<x_{2}\!$	$x>x_{2}\!$
$D>0\!$	$y>0\!$	$y<0\!$	$y>0\!$	$y<0\!$	$y>0\!$	$y<0\!$
$D=0\!$	$y>0\!$	$-\!$	$y>0\!$	$y<0\!$	$-\!$	$y<0\!$
$D<0\!$	$y>0\!$	$-\!$	$y>0\!$	$y<0\!$	$-\!$	$y<0\!$

dengan $x_{1}<x_{2}\!$ merupakan akar-akar persamaan kuadrat. Dalam tabel di atas, apabila $x,x_{1},x_{2}\!$ bersifat kompleks, maka yang dimaksud adalah $\Re \ x$ (nilai riil)-nya.

Geometri

Untuk fungsi kuadrat:

f(x) = x² − x − 2 = (x + 1)(x − 2), dengan variabel x adalah bilangan riil. koordinat-x dari titik-titik di mana kurva menyentuh sumbu-x, x = −1 dan x = 2, adalah akar-akar dari persamaan kuadrat : x² − x − 2 = 0.

Akar-akar dari persamaan kuadrat adalah juga pembuat nol dari fungsi kuadrat tersebut:

f(x)=ax^{2}+bx+c,\,

dikarenakan akar-akar tersebut merupakan nilai $x\,\!$ yang memberikan

f(x)=0.\,

Jika a, b, dan c adalah bilangan riil, dan domain dari $f\,\!$ adalah himpunan bilangan riil, maka pembuat nol dari $f\,\!$ adalah eksak koordinat-x di saat titik-titik tersebut menyentuh sumbu-x.

Mengikuti pernyataan di atas, bahwa jika diskriminan berharga positif, kurva persamaan kuadrat akan menyentuh sumbu-x pada dua buah titik (dua buah titik potong), jika berharga nol, akan menyentuh di satu titik dan jika berharga negatif, kurva tidak akan menyentuh sumbu-x.

Rumus Fungsi Kuadrat

Persamaan fungsi kuadrat : $f(x)=ax^{2}+bx+c\,$ dimana f(x) = y maka titik balik (titik puncak) fungsi kuadrat adalah ( $-{\frac {b}{2a}}\,$ , $-{\frac {D}{4a}}\,$ ).