KEKONGRUENAN DAN KESEBANGUNAN

BAB IV
Konsep Kekongruenan dan Kesebangunan

Kompetensi Inti

3. Pengetahuan 

Memahami dan menerapkan pengetahuan (faktual, konseptual, dan prosedural) berdasarkan rasa ingin tahunya tentang ilmu pengetahuan, teknologi, seni, budaya terkait fenomena dan kejadian tampak mata

4. Keterampilan 

Mengolah, menyaji, dan menalar dalam ranah konkret (menggunakan, mengurai, merangkai, memodifikasi, dan membuat) dan ranah abstrak (menulis, membaca, menghitung, menggambar, dan mengarang) sesuai dengan yang dipelajari di sekolah dan sumber lain yang sama dalam sudut pandang/teori

Kompetensi Dasar 

3.6 Menjelaskan dan menentukan kesebangunan dan kekongruenan antar bangun datar

4.6 Menyelesaikan masalah yang berkaitan dengan kesebangunan dan kekongruenan antar bangun datar

Assalamu`alaikum Wr.Wb. salam jumpa lagi siswa hebat yang sholeh/sholeha kembali, kali ini kita akan pelajaran materi tentang Kekongruenan dan Kesebangunan Bangun Datar, msih ingat kan kalian pernah belajar tentang Bangun Datar yang kalian pelajari di kelas 7 dan 8 ? ya ... ini pun tidak jauh beda  ... kita akan melanjutkan tentang Bangun Datar itu khusus tentang hubungan dua bangun - bangun Datar tersebut. 

Dalam ilmu geometri, terdapat konsep kekongruenan dan kesebangunan. Kekongruenan merujuk kepada dua bangun datar yang memiliki bentuk dan ukuran yang sama. Sementara itu, kesebangunan adalah bangun datar dengan sudut-sudut yang sama besar.Tapi, bagaimana sih penggunaan konsep kekongruenan dan kesebangunan dalam matematika? Yuk kita bahas dalam artikel kali ini.

Kekongruenan

Kekongruenan berlaku pada banyak jenis bangun datar, yang pertama adalah ruas garis. Dua ruas garis kongruen adalah dua garis yang memiliki panjang yang sama. Kekongruenan adalah dua buah bangun datar yang keduanya sama – sama mempunyai bentuk dan ukuran yang sama. Kekongruenan ini di lambangkan dengan simbol 

Perhatikan contoh berikut:

1. Dua Bangun Datar yang Kongruen

Pada kedua bangun di atas adalah bangun yang kongruen, karena panjang KL = PQ, Panjang LM = QR, panjang MN = RS, panjang NK = SP maka oleh karena itu, pada bangun KLMN dan PQRS dapat dikatakan adalah kongruen karena memiliki bentuk dan ukuran yang sama.

2. Dua Segitiga Yang Kongruen

Secara geometris dua segitiga yang kongruen ialah dua segitiga yang saling menutupi dengan tepat. Sifat dua segitiga kongruen tersebut, yaitu:

a. Pasangan sisi yang bersesuaian adalah sama panjang

b. Sudut yang bersesuaian adalahsama besar

Segitiga dapat dikatakan kongruen mana kala dapat memenuhi syarat yskni sebagai berikut:

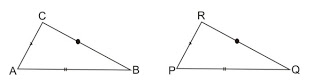
a. Tiga Sisi yang Bersesuaian Sama Besar (sisi, sisi, sisi)

Berdasarkan gambar segitiga ABC dan segitiga PQR di atas, bahwa keduanya memiliki panjang AB = PQ, panjang AC = PR, dan panjang BC = QR. 

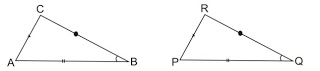
b. Sudut dan Dua Sisi Yang Bersesuaian Sama Besar (sisi, sudut, sisi)

Berdasarkan bangun segitiga ABC dan segitiga PQR di atas, bahwa keduanya mempunyai sisi AB = PQ, ∠B = ∠Q, dan sisi BC = QR

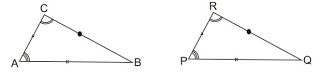
c. Satu Sisi Apit dan Dua Sudut Yang Bersesuaian Sama Besar (sudut, sisi, sudut)

Berdasarkan bangun segitiga ABC dan segitiga PQR di atas bahwa, ∠A = ∠P, sisi AC = PR, dan ∠Q = ∠R

Kesebangunan 

Kesebangunan adalah suatu bangun datar yang mana sudut – sudutnya memiliki kesesuaian yang sama besarnya serta panjang sisi – sisi sudutnya bersesuai yang memiliki sebuah perbandingan yang sama.

Dengan kata lain, kesebangunan adalah dua buah bangun yang mempunyai sudut dan panjang sisi yang sama.

Kesebangunan dilambangkan dengan simbol notasi ≈.

Lihat contoh berikut:

Dua Bangun Datar Yang Sebangun

Bangun datar ini sebangun dengan: Dua bangun datar diatas merupakan dua bangun yang sebangun, dengan beberapa sifat – sifat sebagai berikut:

1. Pasangan Sisi -Sisinya Yang Bersesuaian Memiliki Perbandingan Nilai Yang Sama. Berikut Uraiannya:

• Sisi AD dan KN adalah 
• Sisi AB dan KL adalah  
• Sisi BC dan LM adalah  
• Sisi CD dan MN adalah  

Maka, dapat disimpulkan yaitu :  

2. Besar Sudut Yang Bersesuaian adalah Sama, yaitu;

Dua Bangun Segitiga Yang Sebangun

Perhatikan gambar segitiga berikut:

Bangun segitiga ABC ini sebangun dengan bangun segitiga PQR yakni: 

Dari dua gambar di atas, untuk membuktikan bahwa gambar tersebut adalah sebangun, mdapat kita lihat dengan menguraikan beberapa sifat – sifatnya, yaitu:

1. Perbandingan Antara Sisinya Sama Besar dan Bersesuaian Sama Besar, yaitu:

AC bersesuaian dengan PR yakni:  

AB bersesuaian dengan PQ yakni : 

BC bersesuaian dengan QR yakni:  

Sehingga, dapat disimpulkan bahwa : 

2. Besar Sudut – Sudut Yang Bersesuaian Sama, yaitu: