RABU, 13 MEI 2020

KUIS PERPANGKATAN & BENTUK AKAR

Aneka Kuis Perpangkatan dan Bentuk Akar

 

1. Mari tes kompetensi dengan mengerjakan kuis ini disini ! kuis pertama

2. Kuis ke 2 disini !

 

PEMBAHASAN SOAL KEKONGRUENAN DAN KESEBANGUNAN

Beno mempunyai tinggi badan 150 cm. Dia berdiri pada titik yang berjarak 10 m dari sebuah gedung. Ujung bayangan Beno berimpit dengan ujung bayangan gedung. Apabila panjang bayangan Febri adalah 4 m, maka tinggi gedung itu adalah ….

Pembahasan

Kita perhatikan terlebih dahulu bangun segitiga ABE dan segitiga ACD!
Berdasarkan prinsip kesebangunan, maka dapat kita peroleh 
Sehingga:

Hasilnya yaitu: DC = 5,24 m

Soal 2:

Perhatikan gambar bangun datar berikut:

Berdasarkan bangun persegi panjang ABCD dan PQRS di atas adalah sebagun. Maka tentukanlah:

a. Berapa panjang PQ?
b. Berapa luas dan keliling persegi panjang PQRS?

Pembahasan:

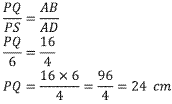
a. Perbandingan sisi AB dengan AD bersesuaian dengan sisi PQ dan PS sehingga:

Maka: panjang PQ adalah 24

b. Mencari luas dan keliling persegi panjang PQRS:

Luas persegi panjang adalah panjang x lebar
Luas persegi panjang PQRS yaitu: PQ x PS = 24 cm x 6 cm = 144 cm2
Keliling persegi panjangnya yaitu:
Keliling persegi panjang PQRS = PQ + QR + RS + SP = 24 cm + 6 cm + 24 cm + 6 cm = 60 cm

Demikianlah pembahasana materi mengenai kesebangunan dan kekongruean. Semoga dapat memberikan manfaat …

KEKONGRUENAN DAN KESEBANGUNAN

BAB IV
Konsep Kekongruenan dan Kesebangunan

Kompetensi Inti

3. Pengetahuan 

Memahami dan menerapkan pengetahuan (faktual, konseptual, dan prosedural) berdasarkan rasa ingin tahunya tentang ilmu pengetahuan, teknologi, seni, budaya terkait fenomena dan kejadian tampak mata

4. Keterampilan 

Mengolah, menyaji, dan menalar dalam ranah konkret (menggunakan, mengurai, merangkai, memodifikasi, dan membuat) dan ranah abstrak (menulis, membaca, menghitung, menggambar, dan mengarang) sesuai dengan yang dipelajari di sekolah dan sumber lain yang sama dalam sudut pandang/teori

Kompetensi Dasar 

3.6 Menjelaskan dan menentukan kesebangunan dan kekongruenan antar bangun datar

4.6 Menyelesaikan masalah yang berkaitan dengan kesebangunan dan kekongruenan antar bangun datar

Assalamu`alaikum Wr.Wb. salam jumpa lagi siswa hebat yang sholeh/sholeha kembali, kali ini kita akan pelajaran materi tentang Kekongruenan dan Kesebangunan Bangun Datar, msih ingat kan kalian pernah belajar tentang Bangun Datar yang kalian pelajari di kelas 7 dan 8 ? ya ... ini pun tidak jauh beda  ... kita akan melanjutkan tentang Bangun Datar itu khusus tentang hubungan dua bangun - bangun Datar tersebut. 

Dalam ilmu geometri, terdapat konsep kekongruenan dan kesebangunan. Kekongruenan merujuk kepada dua bangun datar yang memiliki bentuk dan ukuran yang sama. Sementara itu, kesebangunan adalah bangun datar dengan sudut-sudut yang sama besar.Tapi, bagaimana sih penggunaan konsep kekongruenan dan kesebangunan dalam matematika? Yuk kita bahas dalam artikel kali ini.

Kekongruenan

Kekongruenan berlaku pada banyak jenis bangun datar, yang pertama adalah ruas garis. Dua ruas garis kongruen adalah dua garis yang memiliki panjang yang sama. Kekongruenan adalah dua buah bangun datar yang keduanya sama – sama mempunyai bentuk dan ukuran yang sama. Kekongruenan ini di lambangkan dengan simbol 

Perhatikan contoh berikut:

1. Dua Bangun Datar yang Kongruen

Pada kedua bangun di atas adalah bangun yang kongruen, karena panjang KL = PQ, Panjang LM = QR, panjang MN = RS, panjang NK = SP maka oleh karena itu, pada bangun KLMN dan PQRS dapat dikatakan adalah kongruen karena memiliki bentuk dan ukuran yang sama.

2. Dua Segitiga Yang Kongruen

Secara geometris dua segitiga yang kongruen ialah dua segitiga yang saling menutupi dengan tepat. Sifat dua segitiga kongruen tersebut, yaitu:

a. Pasangan sisi yang bersesuaian adalah sama panjang

b. Sudut yang bersesuaian adalahsama besar

Segitiga dapat dikatakan kongruen mana kala dapat memenuhi syarat yskni sebagai berikut:

a. Tiga Sisi yang Bersesuaian Sama Besar (sisi, sisi, sisi)

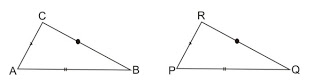
Berdasarkan gambar segitiga ABC dan segitiga PQR di atas, bahwa keduanya memiliki panjang AB = PQ, panjang AC = PR, dan panjang BC = QR. 

b. Sudut dan Dua Sisi Yang Bersesuaian Sama Besar (sisi, sudut, sisi)

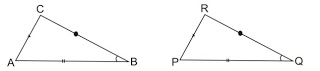
Berdasarkan bangun segitiga ABC dan segitiga PQR di atas, bahwa keduanya mempunyai sisi AB = PQ, ∠B = ∠Q, dan sisi BC = QR

c. Satu Sisi Apit dan Dua Sudut Yang Bersesuaian Sama Besar (sudut, sisi, sudut)

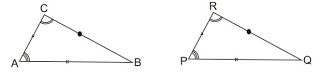
Berdasarkan bangun segitiga ABC dan segitiga PQR di atas bahwa, ∠A = ∠P, sisi AC = PR, dan ∠Q = ∠R

Kesebangunan 

Kesebangunan adalah suatu bangun datar yang mana sudut – sudutnya memiliki kesesuaian yang sama besarnya serta panjang sisi – sisi sudutnya bersesuai yang memiliki sebuah perbandingan yang sama.

Dengan kata lain, kesebangunan adalah dua buah bangun yang mempunyai sudut dan panjang sisi yang sama.

Kesebangunan dilambangkan dengan simbol notasi ≈.

Lihat contoh berikut:

Dua Bangun Datar Yang Sebangun

Bangun datar ini sebangun dengan: Dua bangun datar diatas merupakan dua bangun yang sebangun, dengan beberapa sifat – sifat sebagai berikut:

1. Pasangan Sisi -Sisinya Yang Bersesuaian Memiliki Perbandingan Nilai Yang Sama. Berikut Uraiannya:

• Sisi AD dan KN adalah 
• Sisi AB dan KL adalah  
• Sisi BC dan LM adalah  
• Sisi CD dan MN adalah  

Maka, dapat disimpulkan yaitu :  

2. Besar Sudut Yang Bersesuaian adalah Sama, yaitu;

Dua Bangun Segitiga Yang Sebangun

Perhatikan gambar segitiga berikut:

Bangun segitiga ABC ini sebangun dengan bangun segitiga PQR yakni: 

Dari dua gambar di atas, untuk membuktikan bahwa gambar tersebut adalah sebangun, mdapat kita lihat dengan menguraikan beberapa sifat – sifatnya, yaitu:

1. Perbandingan Antara Sisinya Sama Besar dan Bersesuaian Sama Besar, yaitu:

AC bersesuaian dengan PR yakni:  

AB bersesuaian dengan PQ yakni : 

BC bersesuaian dengan QR yakni:  

Sehingga, dapat disimpulkan bahwa : 

2. Besar Sudut – Sudut Yang Bersesuaian Sama, yaitu:

BANGUN RUANG SISI LENGKUNG ( BRSL )

BAB V

BANGUN RUANG SISI LENGKUNG  ( BRSL )

Kompetensi Inti

3. Pengetahuan 

Memahami pengetahuan (faktual, konseptual, dan prosedural) berdasarkan rasa ingin tahunya tentang ilmu pengetahuan, teknologi, seni, budaya terkait fenomena dan kejadian tampak mata

4. Keterampilan 

Mencoba, mengolah, dan menyaji dalam ranah konkret (menggunakan, mengurai, merangkai, memodifikasi, dan membuat)  dan ranah abstrak (menulis, membaca, menghitung, menggambar, dan mengarang) sesuai dengan yang dipelajari di sekolah dan sumber lain yang sama dalam sudut pandang/teori

Kompetensi Dasar  

3.7 Membuat generalisasi luas permukaan dan volume berbagai bangun ruang sisi lengkung (tabung, kerucut, dan bola)

4.5 Menyelesaikan masalah kontekstual yang berkaitan dengan transformasi geometri (refleksi, translasi, rotasi, dan dilatasi) 

Assalamu`alaikum Wr.Wb. salam jumpa lagi siswa hebat yang sholeh/sholeha tetap semangat, kita lanjut ya ke materi Bangun Ruang Sisi Lengkung, ingatkan ... kalian pernah belajar tentang Bangun Ruang yang dipelajari di kelas delapan tentang Bangun Ruang Sisi Datar ... kini kita lanjut ke Bangun Ruang Sisi Lengkung .... ayo perhatikan dan simak 

Yang dimaksud sebagai bangun ruang sisi lengkung merupakan bangun ruang yang mempunyai sisi lengkung. Sisi lengkung ini sendiri adalah sisi yang membentuk lengkungan kurva. Di dalam materi bangun ruang sisi lengkung hanya terdapat tiga macam bangun ruang yang memiliki sisi lengkung. Diantaranya adalah tabung, kerucut, dan bola

Tabung

Pengertian Tabung

Bangun tabung merupakan suatu bangun ruang tiga dimensi yang mempunyai tutup dan alas yang berbentuk lsebuah ingkaran dengan memiliki ukuran yang sama dan diselimuti oleh persegi panjang.

Unsur-unsur Tabung

                         

a. Sisi

Tabung memiliki 3 sisi yang berbeda, antara lain yaitu sisi atas, sisi bawah dan sisi lengkung (yang kemudian disebut selimut tabung).

Sisi lengkung tabung merupakan sisi yang dibatasi oleh dua bidang sejajar yakni alas serta atas (tutup) yang berbentuk lingkaran yang kongruen (sama bentuk dan ukurannya). Dan memiliki pusat di A dan D.

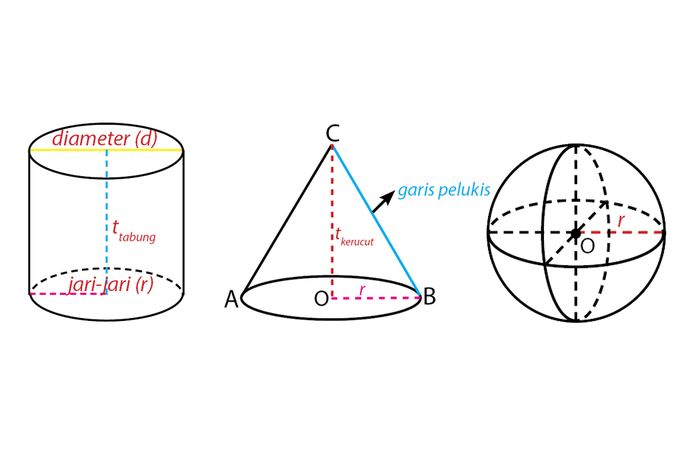
b. Tinggi Tabung

Tinggi tabung merupakan jarak antara bidang alas dan juga bidang tutup pada tabung yang biasa dinotasikan dengan menggunakan huruf t. Berdasarkan dari gambar di atas tinggi tabung tersebut yaitu AD.

c. Jari-jari Tabung

Jari-jari lingkaran biasa dinotasikan dengan huruf (r), sisi alas tabung merupakan CD serta sisi tutup tabung merupakan AB.

d. Diameter tabung

Diameter tabung biasa dinotasikan dengan menggunakan huruf (d). Diameter alas tabung yaitu CC’ serta diameter tutup tabung yaitu BB’.

Sifat Tabung

1. Tabung memiliki 3 buah sisi, 1 persegi panjang, 2 lingkaran.
2. Tidak memiliki rusuk.
3. Tidak memiliki titik sudut.
4. Tidak memiliki bidang diagonal.
5. Tidak memiliki diagonal bidang.
6. tabung memiliki sisi alas serta sisi atas berhadapan yang kongruen.
7. Tinggi tabung merupakan jarak titik pusat bidang lingkaran alas dengan titik pusat lingkaran atas.
8. Bidang tegak tabung berwujud lengkungan yang disebut sebagai selimut tabung.
9. Jaring-jaring tabung berwujud 2 buah lingkaran serta 1 persegi panjang.

Cara Menggambar Tabung

1. Gambar alas tabung memiliki bentuk ellips atau lonjong yang menunjukkan bahwa alas tersebut merupakan dua buah lingkaran.
2. Lalu tarik garis tegak lurus serta sama panjang di kedua tepi lingkaran.
3. Gambar tutup tabung kongruen dengan sisi alas.
   Jadilah gambar tabung.
   Ingat bahwa terdapat bagian tabung yang tidak nampak dari muka, sebab tidak terlihat maka digambar dengan penggunaan garis putus-putus.
4. Luas Permukaan Tabung
   Tabung apabila kita belah pada sisi tegaknya maka akan nampak sisi lengkungnya yang berupa sebuah persegi panjang serta alas tutupnya ialah bangun lingkaran.

Rumus pada Tabung

• Rumus untuk menghitung luas alas:
  luas lingkaran=π x r2
• Rumus untuk menghitung volume pada tabung:
  π x r2 x t
• Rumus untuk menghitung keliling alas pada tabung:
  2 x π x r
• Rumus untuk menghitung luas pada selimut tabung:
  2 x π x r x t
• Rumus untuk menghitung luas pada permukaan tabung:
  2 x luas alas+luas selimut tabung
• Rumus kerucut + tabung:
  • volume = ( π.r2.t )+( 1/3.π.r2.t )
  • luas = (π.r2)+(2.π.r.t)+(π.r.s)

• Rumus tabung + 1/2 bola:
  • Rumus untuk menghitung Volume = π.r2.t+2/3. π.r3
  • Rumus untuk menghitung Luas = (π.r2)+(2.π.r.t)+(½.4.n.r2) = (3.π.r2)+(2. π .r.t)

• Rumus tabung+bola:
  • Rumus untuk menghitung Volume= (π.r2.t)+(4/3. π.r3)
  • Rumus untuk menghitung Luas= (2. π.r2)+(4. π.r2) = π.r2

Keterangan:

• V = Volume tabung(cm3)
• π = 22/7 atau 3,14
• r = Jari – jari /setengah diameter (cm)
• t = Tinggi (cm)

Kerucut

Pengertian Kerucut

Kerucut merupakan salah satu bangun ruang yang memiliki sebuah alas yang berbentuk lingkaran dengan selimut yang mempunyai irisan dari lingkaran.

Di dalam geometri, kerucut merupakan sebuah limas istimewa yang memiliki alas lingkaran. Kerucut mempunyai 2 sisi dan 1 rusuk. Sisi tegak kerucut tidak berwujud segitiga namun berwujud bidang miring yang disebut sebagai selimut kerucut.

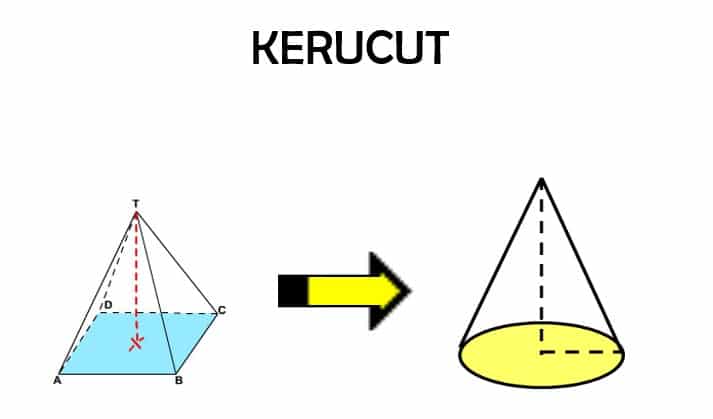
Yang membedakan antara limas dengan kerucut yaitu alas kerucut memiliki bentuk lingkaran, sementara pada limas berbentuk segi n beraturan.

Kecurut bisa dibentuk dari sebuah segitiag siku-siku yang kalian putar 360o, dengan sumbu putar pada sisi siku-sikunya.

Unsur-unsur Kerucut

            

1. Bidang alas, yakni sisi yang berbentuk lingkaran (daerah yang diraster).
2. Diameter bidang alas (d), merupakan ruas garis AB.
3. Jari-jari bidang alas (r), merupakan garis OA serta ruas garis OB.
4. Tinggi kerucut (t), yakni jarak dari titik puncak kerucut ke pusat bidang alas (ruas garis CO).
5. Selimut kerucut, merupakan sisi kerucut yang tidak diraster.
6. Garis pelukis (s), merupakan garis-garis pada selimut kerucut yang ditarik dari titik puncak C ke titik pada lingkaran.

Sifat Kerucut

Terdapat beberapa sifat pada bangun ruang kerucut, antara lain ialah sebagai berikut:

1. Kerucut memiliki 2 sisi.
2. Kerucut tidak  memiliki rusuk.
3. Kerucut memiliki 1 titik sudut.
4. Jaring-jaring kerucut terdiri atas lingkaran serta segitiga.
5. Tidak memiliki bidang diagonal
6. Tidak memiliki diagonal bidang

Rumus pada bangun ruang kerucut

Rumus untuk menghitung volume:
1/3 x π x r x r x t

Rumus untuk menghitung luas:
luas alas+luas selimut

Keterangan:

• r = jari – jari (cm)
• T = tinggi(cm)
• π = 22/7 atau 3,14

Bola

Pengertian Bola

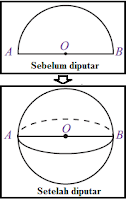
Bola merupakan salah satu bangun ruang sisi lengkung yang dibatasi oleh satu bidang lengkung. Atau juga bisa didefinisikan sebagai sebuah bangun ruang berbentuk setengah lingkaran yang diputar mengelilingi garis tengahnya.

Unsur-unsur Bola

           

1. Titik O dinamakan titik pusat bola.
2. Ruas garis OA dinamakan sebagai jari-jari bola.
3. Ruas garis CD dinamakan sebagai diameter bola. Apabila kalian perhatikan baik-baik, ruas garis AB juga merupakan diameter bola. AB bisa juga dikatakan sebagai tinggi bola.
4. Sisi bola merupakan sekumpulan titik yang memiliki jarak sama kepada titik O. Sisi tersebut dinamakan sebagai selimut atau kulit bola.
5. Ruas garis ACB dinamakan sebagai tali busur bola.
6. Ruas-ruas garis pada selimut bola yakni ACBDA yang juga dinamakan sebagai garis pelukis bola.

Sifat Bola

1. Bola memiliki 1 sisi serta 1 titik pusat.
2. Bola tidak memiliki rusuk.
3. Bola tidak memiliki titik sudut
4. Tidak memiliki bidang diagonal
5. Tidak memiliki diagonal bidang
6. Sisi bola disebut sebagai dinding bola.
7. Jarak dinding ke titik pusat bola disebut sebagai jari-jari.
8. Jarak dinding ke dinding serta melewati titik pusat disebut sebagai diameter.

Rumus pada Bola

Rumus untuk menghitung volume bola yakni:
4/3 x π x r3

Rumus untuk menghitung luas bola yakni:
4 x π x r2

Keterangan:

V : Volume bola (cm3)
L : Luas permukaan bola (cm2)
R : Jari – jari bola (cm)
π : 22/7 atau 3,14